自娱自乐的精神乐园

余凯迪的博客

0%

leetcode_188_contest

发表于 分类于 ， 阅读次数：

5404. 用栈操作构建数组

思路：
如果一个数在最后的数组里，只push；不在最后的数组里面，先push再pop

1
2
3
4
5
6
7
8
9
10
11
12
class Solution:
    def buildArray(self, target: List[int], n: int) -> List[str]:
        res = []
        cur = 1
        for x in target:
            while cur != x:
                res.append('Push')
                res.append('Pop')
                cur += 1
            res.append('Push')
            cur += 1
        return res

5405. 形成两个异或相等数组的三元组数目

思路：
类似前缀和的想法，将前n个数的异或和存储下来，例如$sum[i]= arr[0] \land arr[1] \land … \land arr[i]$，那么从i到j的异或和为 $sum[i-1] \land sum[j]$，另外0和任何数x异或和为x

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution:
    def countTriplets(self, arr: List[int]) -> int:
        pre_sum = [0]
        tmp = 0
        for x in arr:
            tmp ^= x
            pre_sum.append(tmp)
        res = 0
        for i in range(1,len(arr)):
            for k in range(i+1, len(arr)+1):
                for j in range(i+1,k+1):
                    a = pre_sum[i-1] ^ pre_sum[j-1]
                    b = pre_sum[k] ^ pre_sum[j-1]
                    if a==b:
                        res += 1
        return res

5406. 收集树上所有苹果的最少时间

思路：
类似层次遍历，对于每一个需要遍历的节点，从下向根节点回溯；如果该节点没有走过，结果加2，将该节点的父节点加入待遍历的节点；如果之前走过则，则忽略。
对于样例1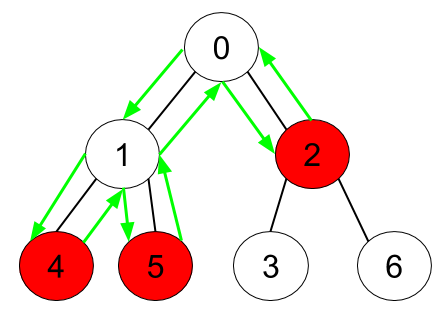

初始时 需要遍历(2,4,5);依次遍历，每次路径长度结果+2，然后将对应的父节点(1,0)加入待遍历节点；此时结果为6；
现在需要遍历(1,0),对于0已经是根节点，可以跳过；对于1，结果+2，将对应的父节点(0)加入待遍历节点；此时结果为8；
最后只剩下(0)，跳过。最终结果为8。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
class Solution:
    def minTime(self, n: int, edges: List[List[int]], hasApple: List[bool]) -> int:
        res = 0
        # 记录每个节点对应的子节点和父节点关系
        children = collections.defaultdict(list)
        father = [-1]*len(hasApple)
        for x in edges:
            children[x[0]].append(x[1])
            father[x[1]] = x[0]
        has_check = set()
        apple_id = []
        for i,x in enumerate(hasApple):
            if x:
                apple_id.append(i)
        t = apple_id
        # 宽搜来进行从下向上依次遍历
        while len(t) > 0:
            # 记录每个节点的父节点
            tt = set()
            for x in t:
                # 当前节点为根节点，跳过
                if x==0:
                    continue
                # 当前节点没有以前没有遇到。将其父节点加入待遍历节点，当前节点置为已遍历到。
                elif x not in has_check:
                    tt.add(father[x])
                    has_check.add(x)
                    res += 2
            # print(t,tt,res)
            t = list(tt)
        return res

5407. 切披萨的方案数

思路：
比较容易想到的方法是直接搜索，递归实现深度优先搜索进行寻找。直接暴力搜索会超时，加入简单的剪枝操作和记忆化搜索可以过。之后想了会用动态规划应该是比较直观的方法，但是动态规划和记忆化的搜索本质上没有太大的区别，都是记录了中间过程的最优方案。
因为每次切完都是拿掉左边和上边的部分，剩余右下的部分，因此可以用剩余pizza的左上角的点的位置，来形象的表示切pizza的操作。
横向切pizza即改变左上角的横坐标，纵向切pizza即改变左上角的纵坐标。
搜索剪枝：对于剩余的pizza，如果横切和纵切所有的可能方案数比k-1小，那么不可能将当前剩余的pizza切成k份。
记忆化：对于同一个pizza，(i,j,k) 可以唯一标识 剩余的pizza需要被切成k份的方案数量。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
class Solution:
    def __init__(self):
        self.counter = {}
    
    def cut(self,pizza,i,j,k):
        # 记忆化搜索
        if (i,j,k) in self.counter:
            return self.counter[(i,j,k)]
        # 递归终止条件
        if k==1:
            # 当前pizza只需要分成1份，只需要判断是否包含苹果（'A'）
            for r in range(i,len(pizza)):
                for c in range(j,len(pizza[0])):
                    if pizza[r][c] == 'A':
                        # print(i,j,r,c)
                        self.res += 1
                        return 1
            return 0
        # 剪枝
        if len(pizza)-i-1 + len(pizza[0])-j-1 < k-1:
            return 0
        num = 0
        # 切的话需要满足上面或者左边的部分包含苹果（'A'）
        # 从上向下遍历，如果前面的行已经出现苹果，之后的行可以省略判断。因此用flag标志是否出现苹果。
        flag = False
        for m in range(i,len(pizza)-1):
            if flag:
                num += self.cut(pizza,m+1,j,k-1)
            else:
                for c in range(j,len(pizza[0])):
                    if pizza[m][c] == 'A':
                        flag = True
                        break
                if flag:
                    num += self.cut(pizza,m+1,j,k-1)
        flag = False
        for m in range(j,len(pizza[0])-1):
            if flag:
                num += self.cut(pizza,i,m+1,k-1)
            else:
                for r in range(i,len(pizza)):
                    if pizza[r][m] == 'A':
                        flag = True
                        break
                if flag:
                    num += self.cut(pizza,i,m+1,k-1)
        self.counter[(i,j,k)] = num
        return num

    def ways(self, pizza: List[str], k: int) -> int:
        return (self.cut(pizza,0,0,k) % int(1e9 + 7))
`